파이썬 머신러닝 4장 모델훈련

4. 모델훈련

1. 선형 회귀

예제) 인당 GDP와 삶의 만족도

\[(\text{삶의만족도}) = \theta_0 + (\text{1인당GDP}) \cdot \theta_1\]

즉, 인당 GDP가 주어지면 위 함수를 사용해 삶의 만족도가 예측이 가능하다.

\[\hat y = \theta_0 + x_1 \cdot \theta_1\]

x1은 인당 gdp, y는 예측된 삶의 만족도의 예측값이다.

선형 회귀 예제: 캘리포니아 주택 가격 예측

\[\hat y = \theta_0 + x_1 \cdot \theta_1 + \cdots + x_{24} \cdot \theta_{24}\]

• $\hat y$: 예측값
• $x_i$: 구역의 $i$ 번째 특성값(위도, 경도, 중간소득, 가구당 인원 등)
• $\theta_0$: 편향
• $\theta_i: (1 \le i \le 24)$번째 특성에 대한 가중치

선형 회귀 모델 함수

선형 회귀 모델을 일반화하면 아래와 같다.

\[\hat y = \theta_0 + x_1 \cdot \theta_1 + \cdots + x_n \cdot \theta_{n}\]

• $\hat y$: 예측값
• $n$: 특성수
• $x_i$: 구역의 $i$ 번째 특성값
• $\theta_0$ : 편향
• $\theta_i:i(1 \le i \le n)$ 번째 특성에 대한 가중치

\[\begin{split}\hat y= 1\cdot \theta_0 + x_1 \cdot \theta_1 + \cdots + x_n \cdot \theta_{n}= [1, x_1, \dots, x_n]\, \begin{bmatrix}\theta_0\\\theta_1 \\\vdots \\\theta_n\end{bmatrix}\end{split}\]

선형 회귀 모델의 행렬 연산 표기법

X가 전체 입력 데이터셋, 전체 훈련셀을 가리키는(m, 1 + n)모양의 2D어레이, 즉 행렬이라 하면

• m: 훈련셋 크기

• n: 특성 수

  \[\hat{\mathbf y} = \begin{bmatrix} \hat y_1 \\ \vdots \\ \hat y_m \end{bmatrix} = \begin{bmatrix} [1, x_1^{(1)}, \dots, x_n^{(1)}] \\ \vdots \\ [1, x_1^{(m)}, \dots, x_n^{(m)}] \\ \end{bmatrix} \begin{bmatrix} \theta_0\\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}\]

i번째 입력 샘플의 1차원 어레이는 아래와 같다.

\[\mathbf{x}^{(i)} = [1, x_1^{(i)}, \dots, x_n^{(i)}]\]

모든 입력값에 대한 예측값을 아래 행렬식으로 표현이 가능하다.

\[\begin{aligned} \hat{\mathbf y} &= \begin{bmatrix} \hat y_1 \\ \vdots \\ \hat y_m \end{bmatrix} \\ &= \begin{bmatrix} [1, x_1^{(1)}, \dots, x_n^{(1)}] \\ \vdots \\ [1, x_1^{(m)}, \dots, x_n^{(m)}] \\ \end{bmatrix} \, \begin{bmatrix} \theta_0\\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix} \end{aligned}\]

식으로 줄이면 아래와 같다.

\[\hat{\mathbf y} = \mathbf{X}\, \mathbf{\theta}\]

식에 사용된 기호들은 아래와 같다.

데이터	어레이 기호	어레이 모양(shape)
모든 예측값	$\hat y$	$(m, 1)$
훈련셋	$X$	$(m, 1 + n)$
모델 파라미터	$\theta$	$(1 + n, 1)$

비용 함수: 평균 제곱 오타(MSE)

회귀모델의 일반적인 비용함수

모델의 성능이 얼마나 나쁜지 평가

⇒ 값이 작을수록 성능이 좋음

• MSE를 사용한 선형 회귀 모델 성능 평가

\[MSE(\theta) = \frac{1}{m} \sum_{i=1}^{m} (x^{(i)} \theta - y^{(i)})^2\]

위 공식은 실제 예측값을 나타낸다.

| m | 데이터 샘플의 개수 | | — | — | | i | 각각의 데이터 샘플 | | x | i번째 데이터 샘플의 값 |

• 최종 목표: MSE가 최소가 되도록 하는 세타 찾기
• 선형회귀의 경우 0으로 지속적으로 줄어든다.

MSE(θ)최소화

방식 1: 정규방정식 또는 특이값 분해(SVD) 활용

• 드물지만 수학적으로 비용 함수를 최소화하는 θ 값을 직접 계산할 수 있는 경우 활용.
• 계산복잡도가 O(n²) 이상인 행렬 연산을 수행해야 하기에 특성의 개수 n이 매우 큰 경우 컴퓨터로 처리 불가

• 정규 방정식

  \[\hat\theta = (X^{T} X)^{-1}X^Ty\]
  • 복잡도는 O(n²)임
  • 입력 변수 X와 타겟 값 Y의 행렬을 이용하여 가중치 θ를 직접 구하는 방식
  • 모든 학습 데이터를 고려해 파라미터를 찾아내는 방법

• SVD 활용

  \[\hat\theta = X + y\]
  • 복잡도가 O(n²)으로 정규방정식보다 좀 더 빠름
  • 입력 데이터의 차원을 축소, 행렬의 랭크를 파악 가능

2. 경사하강법

비용함수(cost function)를 최소화 하기위해 경사를 반복적으로 하강해가면서 파라미터를 조정해 나가는 것

• 기본 아이디어
  • 반복적인 계산을 통해 MSE를 최소화하는 가중치를 찾는 방법
  • 특성 또는 훈련 샘플이 아주 많은 경우 적용
  • 선형 회귀 모델 훈련에 일반적으로 적용되는 기법
• 주요 개념
  • 최적 학습 모델
    • 비용함수를 최소화하는 또는 효용함수를 최대화하는 파라미터를 사용하는 모델
    • 경사를 반복적으로 하강해가면서 파라미터를 조정
    • 학습률 하이퍼 파라미터 = 하강하는 보폭을 의미
  • 파라미터

    • 선형 회귀 모델에 사용되는 편향과 가중치 파라미터처럼 모델 훈련중에 학습되는 파라미터를 가리킨다.

      \[θ = [\theta_0, \theta_1, ..., \theta_n]\]
  • 비용함수
    • 모델의 예측값과 실제값의 차이

    • MSE처럼 모델이 얼마나 나쁜지 측정

      \[\mathrm{MSE}(\mathbf{\theta}) = \frac 1 {m_b} \sum_{i=1}^{m_b} \big(\mathbf{x}^{(i)}\, \mathbf{\theta} - y^{(i)}\big)^2\]
  • 전역 최솟값
    • 비용 함수의 전역 최소값
  • 비용 함수의 그레이디언트 벡터
    • 다변수 함수의 미분값

    • 그레이디언트가 가리키는 반대 방향으로 움직여야 가장 빠르게 전역 최솟값에 접근

      \[\begin{split}\nabla_\mathbf{\theta} \textrm{MSE}(\mathbf{\theta}) =\begin{bmatrix}    \frac{\partial}{\partial \mathbf{\theta}_0} \textrm{MSE}(\mathbf{\theta}) \\    \frac{\partial}{\partial \mathbf{\theta}_1} \textrm{MSE}(\mathbf{\theta}) \\    \vdots \\    \frac{\partial}{\partial \mathbf{\theta}_n} \textrm{MSE}(\mathbf{\theta})\end{bmatrix}\end{split}\]
  • 학습률
    • 훈련 과정에서의 비용함수 파라미터 조정 비율
• 에포크
  • 경사하강법에서 훈련 세트를 한 번 모두 사용하는 과정
• 허용오차
  • 비용함수의 값이 허용오차보다 작아지면 훈련 종료

선형 회귀 모델과 경사하강법

MSE를 비용 함수로 사용하는 경우 경사하강법은 다음 과정으로 이루어진다.

1. θ를 임의의 값으로 지정한 후 훈련을 시작한다.
2. 아래 단계를 MSE(θ)가 허용오차보다 적게 작아지는 단계까지 반복한다.
   • 배치 크기 mb 만큼의 훈련 샘플을 이용하여 예측값 생성 후 MSE(θ)계산.

   • 아래 점화식을 이용한 θ업데이트

     \[\theta^{(\text{new})} = \theta^{(\text{old})}\, -\, \eta\cdot \nabla_\theta \textrm{MSE}(\theta^{(\text{old})})\]

기울기 벡터의 방향과 크기

그레이디언트 벡터의 방향과 크기

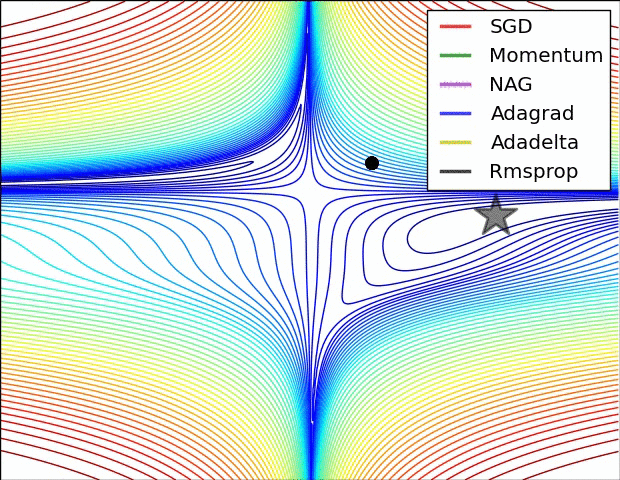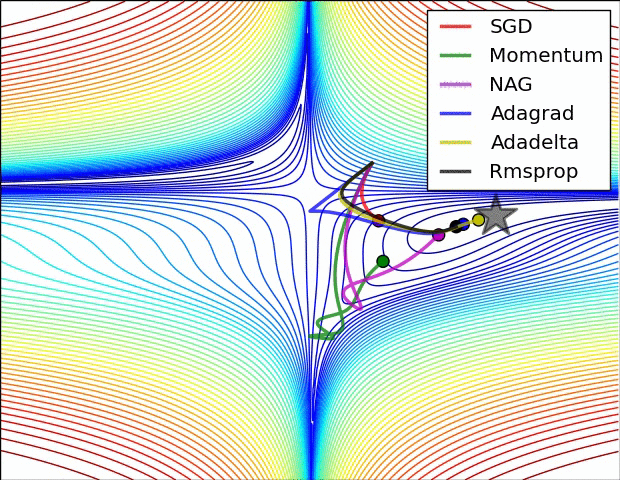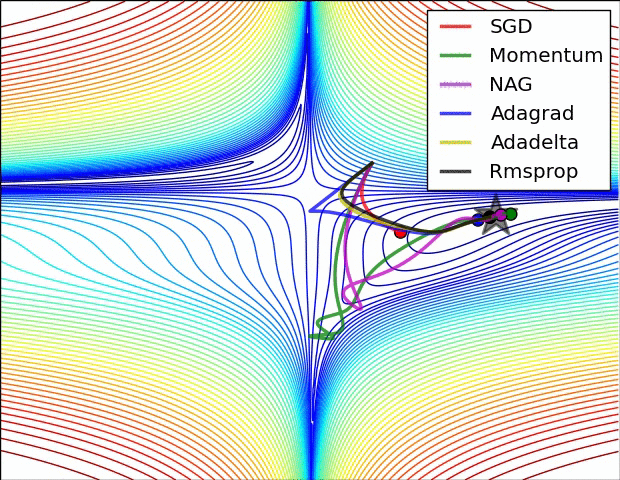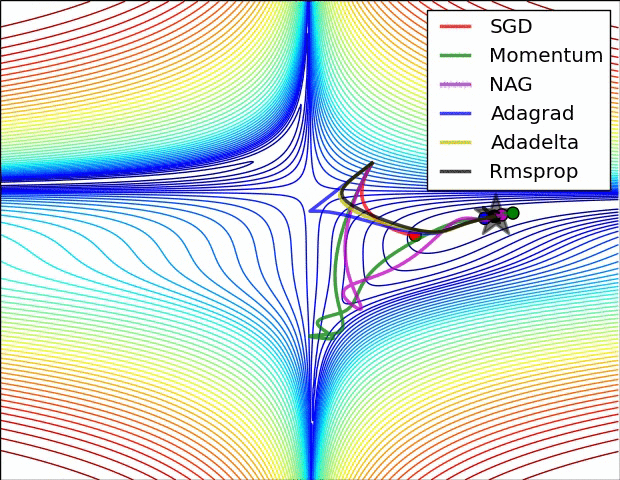
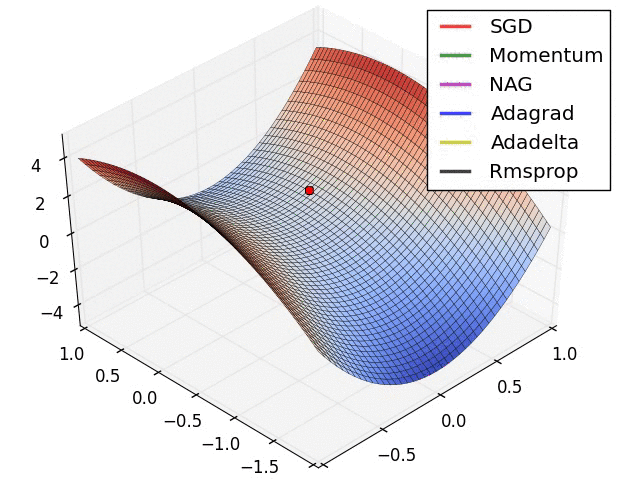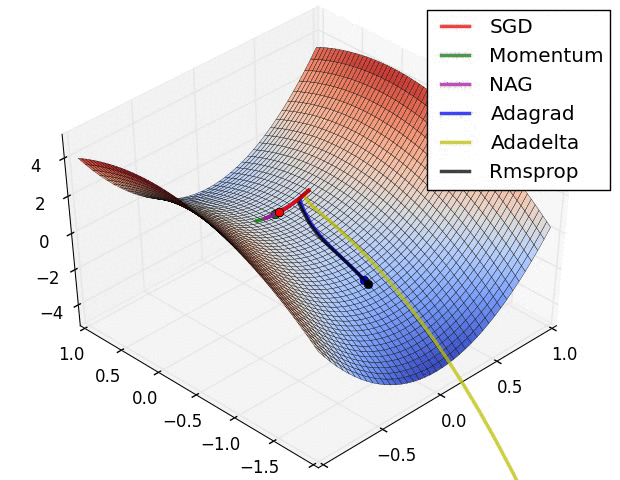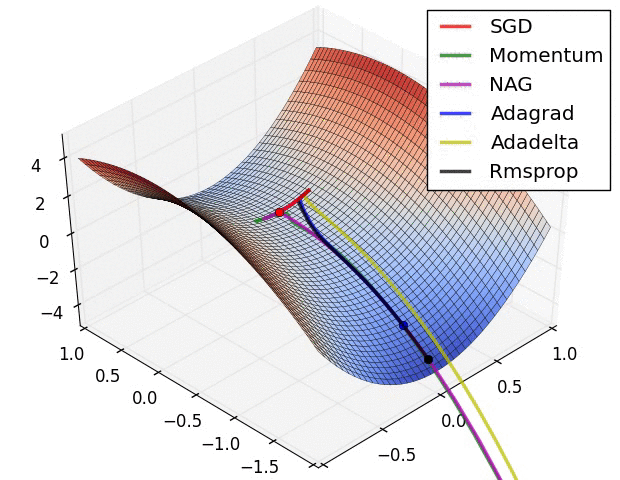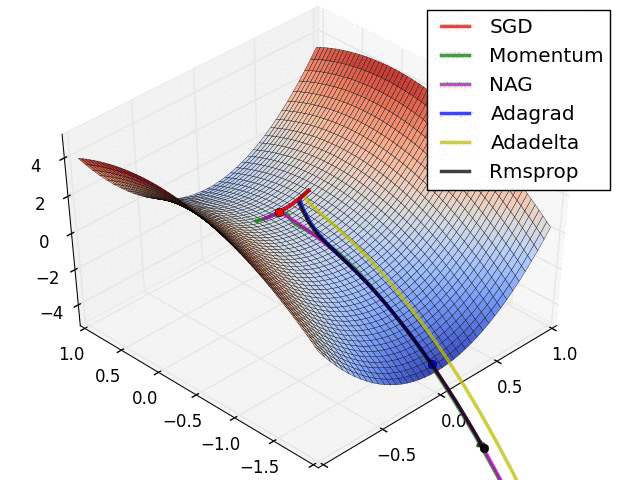
위 gif들은 경사하강법과 최적화 알고리즘에 대한 시각화다.

학습률의 중요성

적절한 학습률

학습률이 작은경우

• 학습률이 너무 작으면 최적점에 도달하는데 시간이 오래 걸림

학습률이 많은경우

• 학습률이 너무 많으면 최적점을 지나칠 수 있음

학습률에 따른 선형 회귀 모델이 최적의 모델로 수렵하는지 여부와 수렴 속도가 달라지는 것을 보여주는 그림

• n = 0.02 → 학습률이 작음
• n = 0.1 → 학습률이 적절함
• n = 0.5 → 학습률이 큼

3. 다항 회귀

• 다항 회귀(polynomial regression)란?
  • 선형 회귀를 이용하여 비선형 데이터를 학습하는 기법
  • 즉, 비선형 데이터를 학습하는 데 선형 모델 사용을 가능하게 함.
• 기본 아이디어
  • 특성들의 조합 활용
  • 특성 변수들의 다항식을 조합 특성으로 추가

선형 회귀 대 다항 회귀

• 선형 회귀: 1차 선형 모델

  \[\hat y = \theta_0 + \theta_1\, x_1\]

  

• 다항 회귀: 2차 다항식 모델

  \[\hat y = \theta_0 + \theta_1\, x_1 + \theta_2\, x_{1}^2\]

  

  • 2차 다항 회귀 모델은 주어진 데이터에 대해 최적의 계수를 추정하기 위해 최소 제곱법(Least Squares Method)을 이용하여 모델을 훈련시킵니다.
  • 최소 제곱법은 예측값과 실제값의 차이인 잔차(residual)를 최소화하는 방향으로 계수를 업데이트하는 방법입니다.
  • 2차 다항 회귀 모델은 비선형적인 데이터에 대해 더 적합한 모델링을 가능하게 하지만, 차수가 높아질수록 과적합(Overfitting)의 위험이 증가하게 됩니다.
  • 따라서, 적절한 차수를 선택하는 것이 중요합니다.

4. 학습 곡선

모델 성능 평가: 교차 검증 vs 학습 곡선

모델 성능 평가는 2가지가 있다.

1. 교차 검증
   • 과소적합: 훈련셋에 대한 성능 평가와 교차 검증 점수 모두 낮은 경우
   • 과대적합: 훈련셋에 대한 성능 평가는 우수하지만 교차 검증 점수가 낮은 경우
2. 학습 곡선 (learning curve)
   • 훈련셋와 검증셋에 대한 모델 성능을 비교하는 그래프
     • x-축: 훈련셋 크기. 훈련셋의 크기를 1%에서부터 출발해서 점차 키워 나가면서 모델 성능 평가
     • y-축: 훈련셋 크기에 따른 모델 성능. 훈련 점수와 검증 점수 사용
   • 학습 곡선의 모양에 따라 과소적합/과대적합 판정 가능
   • sklearn.model_selection 모듈의 learning_curve() 함수를 이용해서 쉽게 시각화 가능

과소적합 / 과대적합 판정

• 예제: 선형 모델, 2차 다항 회귀 모델, 300차 다항 회귀 모델 비교
• 다항 회귀 모델의 차수에 따라 훈련된 모델이 훈련셋에 과소 또는 과대 적합할 수 있음.

학습 곡선 특징

1. 과소적합 모델에서의 학습 곡선

   

   • 2차 다항 함수의 분포를 따르는 데이터셋에 LinearRegression 모델을 적용한 학습 곡선
     • 훈련셋에 대한 성능(빨강): 훈련셋이 커지면서 RMSE(평균 제곱근 오차)가 커지면서 어느 순간 변화 없음
     • 검증셋에 대한 성능(파랑): 검증셋에 대한 성능이 훈련셋에 대한 성능과 거 의 비슷해짐

2. 과대적합 모델에서의 학습 곡선

   

   • 2차 다항 함수의 분포를 따르는 데이터셋에 10차 다항회귀 모델을 적용한 학습 곡선
     • 훈련셋에 대한 성능(빨강): 훈련셋에 대한 평균 제곱근 오차가 매우 낮음.
     • 검증셋에 대한 성능(파랑): 훈련셋에 대한 성능과 차이가 크게 벌어짐.
   • 과대적합 모델 개선법: 훈련 데이터 추가. 하지만 일반적으로 매우 어렵거나 불가능.

편향 vs 분산

• 편향
  • 데이터셋에 대한 모델링이 틀린 경우
  • 예를 들어 실제로는 2차원 모델인데 1차원 모델을 사용하는 경우 발생
  • 과소적합 발생 가능성 높음.
• 분산
  • 모델이 훈련 데이터에 민감하게 반응하는 정도
  • 고차 다항 회귀처럼 자유도(degree of freedom)가 높은 모델일 수록 분산이 커짐
    • 모델의 자유도: 모델이 찾아야 하는 파라미터의 개수
  • 과대적합 발생 가능성 높음.

편향과 분산의 트레이드 오프

• 복잡한 모델일 수록 편향을 줄고 분산은 커짐.
• 단순한 모델일 수록 편향은 커지고 분산은 줄어듦

모델 일반화 오차

• 훈련 후에 새로운 데이터 대한 예측에서 발생하는 오차.
• 모델의 일반화 성능은 일반화 오차가 낮을수록 높음.
• 오차 발생 원인
  • 편향
  • 분산
  • 줄일 수 없는 오차: 데이터 자체가 갖고 있는 잡음(noise) 때문에 발생하는 어쩔 수 없는 오차
• 결론: 일반화 오차를 줄이기 위해 모델의 편향 또는 분산 둘 중에 하나에 집중해야 함.

5. 모델 규제

자유도와 규제

• 자유도 (degree of freedom): 학습 모델 결정에 영향을 주는 요소(특성)들의 수
  • 선형 회귀: 특성 수
  • 다항 회귀: 특성 수 + 차수
• 규제 (regularization): 자유도 제한
  • 선형 회귀 모델 규제: 가중치 역할 제한, 가중치의 절댓값 줄이기
  • 다항 회귀 모델 규제: 차수 줄이기, 가중치의 개수 줄이기

선형 회귀 모델 규제 방법

• 1. 릿지 회귀(세타를 제한함)

  • 비용함수

    

  • mb: 배치 크기
  • α(알파): 규제 강도 지정.
    • α = 0: 규제가 전혀 없는 기본 선형 회귀
    • α가 커질 수록 가중치의 역할이 줄어듦. 비용을 줄이기 위해 가중치를 작게 유지하는 방향으로 학습. 따라서 모델의 분산 정도가 약해짐.
  • 가중치(θ0)은 규제하지 않음
  • 주의사항: 특성 스케일링 전처리를 해야 규제 모델의 성능이 좋아짐.

  

  • 릿지 규제를 적용한 6 가지 경우: 분산 줄고 편향 늘어남.
    • 왼편: 선형 회귀 모델에 세 개의 값 적용.
    • 오른편: 10차 다항 회귀 모델에 세 개의 값 적용.
• 2. 라쏘 회귀(세타를 작게 만듦)

  • 비용함수

    

  • α(알파): 규제 강도 지정. α = 0 이면 규제가 전혀 없는 기본 선형 회귀
  • 덜 중요한 특성을 무시하기 위해 해당 특성의 가중치 ∣θi∣를 보다 빠르게 0에 수렴하도록 유도. 또한 기본적으로 ∣θi∣가 가능하면 작게 움직이도록 유도.
  • 가중치(θ0)은 규제하지 않음

  • 라쏘 규제

    

    • 라쏘 규제를 적용한 적용한 6 가지 경우
      • 왼편: 선형 회귀 모델에 세 개의 값 적용.
      • 오른편: 10차 다항 회귀 모델에 세 개의 값 적용.
• 3. 엘라스틱 넷 회귀(위 두개 다 가능)
  • 비용함수
  • 릿지 회귀와 라쏘 회귀를 절충한 모델
  • 혼합 비율 을 이용하여 릿지 규제와 라쏘 규제를 적절하게 조절

규제 선택

• 대부분의 경우 약간이라도 규제 사용 추천
• 릿지 규제가 기본
• 유용한 속성이 많지 않다고 판단되는 경우
• 라쏘 규제나 엘라스틱 넷 활용 추천
• 불필요한 속성의 가중치를 0으로 만들기 때문
• 특성 수가 훈련 샘플 수보다 많거나 특성 몇 개가 상호 강하게 연관되어 있는 경우엔 엘라스틱 넷 추천

조기 종료

• 모델이 훈련 중에 훈련셋에 너무 과하게 적응하지 못하도록 하는 가장 일반적인 규제 기법
• 에포크가 남아있다 하더라도 검증셋 대한 비용함수의 값이 줄어 들다가 다시 커지는 순간 훈련 종료
• 검증셋에 대한 비용 함수의 곡선이 진동이 발생할 있기에 검증 손실이 한동안 최솟값보다 높게 유지될 때 훈련 멈추고 기억해둔 최적의 모델 사용

확률적 경사하강법과 조기 종료

아래 코드는 SGDRegressor 모델에 조기 종료를 지정한다.

• penalty='elasticnet' : 엘라스틱 넷 회귀 적용
• alpha=0.1 : 규제 강도
• l1_ratio=0.5 : 라쏘 규제 비율
• eta0=0.002 : 학습률
• early_stopping=True : 조기 종료 실행. 훈련셋의 일부를 검증셋으로 활용.
• max_iter=1000 : 최대 훈련 에포크
• tol=1e-3 : 훈련 점수 또는 검증 점수가 지정된 값 이하로 최대 n_iter_no_change 에포크 동안 변하지 않으면 조기 종료 실행
• n_iter_no_change=5 : 훈련 점수 또는 검증 점수가 지정된 에포크 동안 얼마나 변하는지 확인

6. 로지스틱 회귀

로지스틱 회귀와 소프트맥스 회귀

• 회귀 모델을 분류 모델로 활용
• 이진 분류: 로지스틱 회귀 사용
• 다중 클래스 분류: 소프트맥스 회귀 사용

확률 계산: 시그모이드 함수

• 시그모이드 함수 활용

  \[\hat p = h_\theta(\mathbf{x}) = \sigma(\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n)\]

• 로지스틱 회귀 모델에서 샘플 가 양성 클래스에 속할 확률 p^ = hθ(x) = σ(θ0 + θ1 x1 + ⋯ + θn xn)
• p^의 값은 확률이기 때문에 0 ~ 1사이의 값을 출력해냄

예측값

\[\begin{split}\hat y = \begin{cases}0 & \text{if}\,\, \hat p < 0.5 \\[1ex]1 & \text{if}\,\, \hat p \ge 0.5\end{cases}\end{split}\]

• 양성 클래스인 경우:

  \[\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n \ge 0\]

• 음성 클래스인 경우:

  \[\theta_0 + \theta_1\, x_1 + \cdots + \theta_n\, x_n < 0\]

비용함수

• 비용함수: 로그 손실log loss 함수 사용

\[J(\theta) = - \frac{1}{m_b}\, \sum_{i=1}^{m_b}\, \left( y^{(i)} \cdot \log(\,\hat p^{(i)}\,) + (1-y^{(i)}) \cdot \log(\,1 - \hat p^{(i)}\,)\right)\]

• 모델 훈련: 위 비용함수에 대해 경사 하강법 적용

로그 손실 함수 이해

• 틀린 예측을 하면 손실값이 무한이 커짐
• 왼쪽 그림: 샘플의 레이블이 1(양성)인데 예측 확률( )이 0에 가까운 경우 로그 손실이 매우 클 수 있음
• 오른쪽 그림: 샘플의 레이블이 0(음성)인데 예측 확률( )이 1에 가까운 경우 로그 손실이 매우 클 수 있음

붓꽃 데이터셋

• 붓꽃의 품종 분류를 로지스틱 회귀로 진행
• 붓꽃 데이터셋의 샘플의 특성 4개:
  • 꽃받침sepal의 길이와 너비,
  • 꽃입petal의 길이와 너비

붓꽃 데이터셋의 레이블

• 0: Iris-Setosa(세토사)
• 1: Iris-Versicolor(버시컬러)
• 2: Iris-Virginica(버지니카)

붓꽃 데이터셋 불러오기

사이킷런 자체 제공

from sklearn.datasets import load_iris
iris = load_iris(as_frame=True )

Bunch자료형

• load_iris() 함수는 데이터셋을 사전 자료형과 유사한 Bunch 자료형으로 불러온다.
• Bunch 자료형은 키를 사용한 인덱싱을 마치 클래스의 속성을 확인하는 방식으로 다룰 수 있음
  • 예제: iris['data'] 대시 iris.data 사용 가능
• data 키: 4개의 특성으로 구성된 훈련셋 데이터프레임
• target 키: 레이블셋 시리즈

iris.data.head(5)

     sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0    5.1               3.5              1.4               0.2
1    4.9               3.0              1.4               0.2
2    4.7               3.2              1.3               0.2
3    4.6               3.1              1.5               0.2
4    5.0               3.6              1.4               0.2

결정 경계: 꽃잎의 너비 기준 Iris-Virginica 여부 판정

X = iris.data[["petal width (cm)"]].values
y = iris.target_names[iris. target] == 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)

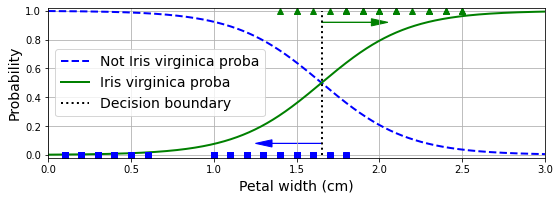
결정 경계: 꽃잎의 너비, 길이 기준 Iris-Virginica 여부 판정

X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = iris.target_names[iris. target] = = 'virginica'
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

log_reg = LogisticRegression(C=2, random_state=42)
log_reg.fit(X_train, y_train)

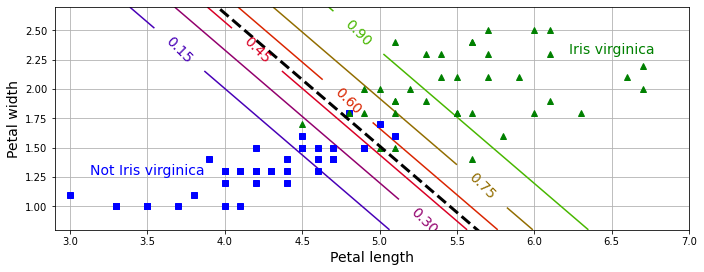
로지스틱 회귀 규제하기

• 하이퍼파라미터 penalty 와 C 이용
• enalty
  • l1 , l2 , elasticnet 세 개중에 하나 사용.
  • 기본은 l2 , 즉, 규제를 사용하는 릿지 규제.
  • elasticnet 을 선택한 경우 l1_ration 옵션 값을 함께 지정.
• C
  • 릿지 또는 라쏘 규제 정도를 지정하는 의 역수에 해당.
  • 따라서 0에 가까울 수록 강한 규제 의미.

소프트맥스(softmax) 회귀

• 로지스틱 회귀 모델을 일반화하여 다중 클래스 분류를 지원하도록 한 회귀 모델
• 다항 로지스틱 회귀 라고도 불림
• 주의사항: 소프트맥스 회귀는 다중 출력 분류 지원 못함. 예를 들어, 하나의 사진에서 여러 사람의 얼굴 인식 불가능.

소프트맥스 회귀 학습 아이디어

• 샘플 x = [x1, ….., xn]가 주어졌을 때 각각의 분류 클래스 k에 대한 점수 sk(x) 계산. 즉, k*(n+1) 개의 파라미터를 학습시켜야 함.

\[s_k(\mathbf{x}) = \theta_0^{(k)} + \theta_1^{(k)} x_1 + \cdots + \theta_n^{(k)} = [1, x_1, \dots, x_n]\, \begin{bmatrix} \theta_0^{(k)}\\ \theta_1^{(k)} \\ \vdots \\ \theta_n^{(k)} \end{bmatrix}\]