2. 신경망 기본 구성 요소
1. 신경망 모델 기초 훈련법
케라스 라이브러리를 이용하여
MNIST 손글씨 데이터셋을 대상으로 분류를 학습하는
신경망 모델을 구성, 훈련, 활용하는 방법을 소개
훈련셋 준비: MNIST 데이터셋
1
2
3
from tensorflow.keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
-
손글씨 숫자 인식 용도 데이터셋. 28x28 픽셀 크기의 사진 70,000개의 샘플로 구성
라벨: 0부터 9까지 10개의 클래스 중 하나
-
데이터를 2가지 종류로 나눠서 사용
- 훈련셋: 샘플 60,000개 (모델 훈련용)
train_imagestrain_labels
- 테스트셋: 샘플 10,000개 (훈련된 모델 성능 테스트용)
test_imagestest_labels
- 훈련셋: 샘플 60,000개 (모델 훈련용)
하나의 샘플

그림 출처: Towards data science: Mikkel Duif(2019)
그림은 좌측 숫자 7을 픽셀로 색칠된 정도에 따라 수치가 정해지고, 우측에 숫자를 예측한 표가 있다.
그림에 나온 샘플은 7을 99%, 3을 1%의 확률로 예측하고 있다는것을 알 수 있다.
-
샘플, 타깃, 라벨, 예측값, 클래스
- 샘플
- 타깃과 라벨
- 타깃: 개별 샘플과 연관된 값이며, 샘플이 주어지면 머신러닝 모델이 맞춰야 하는 값임.
- 라벨: 분류 과제의 경우 타깃 대신 라벨이라 부름.
- 예측값
- 클래스(범주)
- 분류 모델의 에측값으로 사용될 수 있는 라벨(타깃)들의 집합
신경망 모델 지정
1
2
3
4
5
6
7
from tensorflow import keras
from tensorflow.keras import layers
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
keras를 사용해서 모델을 구성함layers와Sequential라는 모델을 가지고 있는 패키지임Sequential: 순차 모델Dense층- 입력 샘플의 모든 특성을 이용하여 층의 출력값을 생성함. 이런 방식으로 연결된 층들을 조밀하게 연결된densely connected 또는 완전하게 연결된fully-connected 층이라고 함.
Dense층은 항상 조밀하게 다음 층과 연결됨. - 첫째
Dense층- 512개의 유닛 사용. 784개의 픽셀 값으로부터 512개의 값을 생성. 즉, 한 장의 MNIST 손 글씨 숫자 사진에 해당하는 길이가 784인 1차원 어레이가 입력되면 길이가 512인 1차원 배열을 생성함.
- 렐루$_{Relu }$ 함수: 활성화 함수로 사용됨. 생성된 512개의 값 중에서 음수는 모두 0으로 처리하는 함수.
- 둘째
Dense층- 10개의 유닛 사용. 입력된 512개의 값으로부터 10개의 값을 생성.
- 유닛을 10개로 지정했기 때문에 회귀모델은 아니란걸 알 수 있음 (단순 선형 회귀 모델은 1개의 결과를 도출)
- 소프트맥스$_{Softmax }$ 함수가 활성화 함수로 사용됨.
- 계산된 10개의 값을 이용하여 0부터 9까지 10개의 범주 각각에 속할 확률을 계산함. 모든 확률의 합은 1.
- 입력 샘플의 모든 특성을 이용하여 층의 출력값을 생성함. 이런 방식으로 연결된 층들을 조밀하게 연결된densely connected 또는 완전하게 연결된fully-connected 층이라고 함.
신경망 모델 컴파일
1
2
3
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
optimizer- 경사하강법(백워드 패스, 역전파) 업무를 처리하는 옵티마이저 지정.
rmsprop가 경사하강법을 처리해줌- 경사하강법을 사용하면 모델 가중치 최적화, 손실 함수 최소화를 해주기 때문에 사용한다.
loss- 손실 함수$_{loss \ function}$ 지정.
- 손실 함수: 모델 훈련하는 동안 모델의 성능을 손실값으로 측정. 손실값이 작을 수록 좋음.
metrics- 훈련과 테스트 과정을 모니터링 할 때 사용되는 한 개 이상의 평가 지표$_{metric}$를 포함하는 리스트로 지정. 리스트로 지정했기 때문에 여러 평가 지표가 들어갈 수 있음
- 손실 함수값, 정확도 등 모델의 종류에 따라 다양한 평가 지표를 사용할 수 있음.
- 분류 모델의 경우 일반적으로 정확도를 평가지표로 포함시킴.
- 평균 제곱근 오차$_{RMSE}$: 평가 기준
-
데이터 전처리
- 머신러닝 모델에 따라 입력값이 적절한 형식을 갖춰야 함
- 앞서 두 개의
Dense층과Sequential클래스로 지정된 모델의 입력값은 1차원 어레이 형식을 갖춰야 함.
1
2
3
4
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255 # 0과 1사이의 값
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype("float32") / 255 # 0과 1사이의 값
- 현재 기존 데이터의 모양은 3차원 배열로 (60000, 28, 28)의 모양을 띈다.
- 데이터를
reshape를 사용해서 2차원 배열(60000, 28 * 28)로 바꿔준다.
모델 훈련
1
model.fit(train_images, train_labels, epochs=5, batch_size=128)
- 첫째 인자: 훈련 데이터셋
- 둘째 인자: 훈련 라벨셋
epoths: 에포크. 전체 훈련 세트 대상 반복 훈련 횟수.-
batch_size: 배치 크기. 배치 크기만큼의 훈련 데이터셋로 훈련할 때 마다 가중치 업데이트. -
모델의 훈련 과정
-
에포크가 끝날 때마다 평균 손실값과 평균 정확도 출력

- 첫 에포크의 경우 8초가 걸렸고, 1개의 스탭당 12ms가 걸렸으며, 손실은 0.2648이 발생했지만, 정확도는 0.9233 이란걸 알 수 있다.
- 배치가 469인 이유는 60000을 위에 사용한 배치 크기인 128로 나누면 468.75개의 배치가 생성되기 때문이다. 즉, 1개의 에포크당 468번의 스탭이 실행된다.
-
5개의 에포크의 결과가 나오고 평균을 계산하면 최종적으로 훈련셋에 대한 평균 오차, 정확도 등을 알 수 있다.
-
배치 크기, 스텝, 에포크
- 스텝
- 하나의 배치(묶음)에 대해 훈련하는 과정
- 스텝이 끝날 때마다 사용된 배치 묶음에 대한 손실값과 정확도가 계산
- 에포크$_{epoch}$: 훈련셋 전체에 대해 한 번 모델 예측과 가중치 조정을 실행하는 과정
- MNIST 데이터셋 예제
- 배치 크기(
batch_size)가 128이기에 총 6만개의 훈련 샘플을 128개씩 묶음 - 따라서 469(60,000/128 = 468.75)개의 배치 생성
- 하나의 에포크 동안 총 469번의 스텝이 실행
- 배치 크기(
- 스텝
-
- 모델 예측값 계산 과정
1
2
3
4
5
6
7
8
9
10
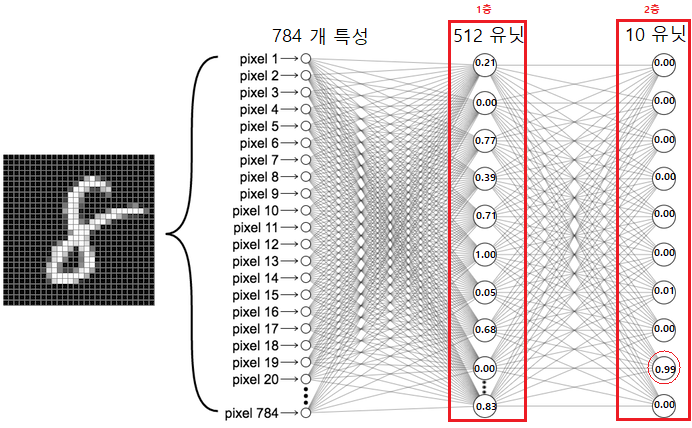
- 위에 신경망 모델 지정에서 `Dense`층을 선언할 때 512와 10을 유닛으로 지정했다.
- 손글씨 데이터 샘플 입력
- 위 사진에서는 8을 가리키는 사진 샘플이 입력값으로 사용됨.
- 784 개의 픽셀값으로 구성된 1차원 어레이로 변환
- 첫째 `Dense` 층
- 입력된 784개의 픽셀값을 이용하여 512개의 값 생성.
- `relu()` 활성화 함수로 인해 음수는 모두 0으로 처리됨.
- 둘째 `Dense` 층
- 첫째 `Dense` 층에서 생성된 512개의 값을 이용하여 10개의 값 생성.
- `softmax()` 활성화 함수로 인해 모두 0과 1사이의 값으로 변환됨. 모든 값의 합이 1이 되며, 각각의 범주에 속할 확률을 가리킴.
- 가중치 행렬과 출력값 계산
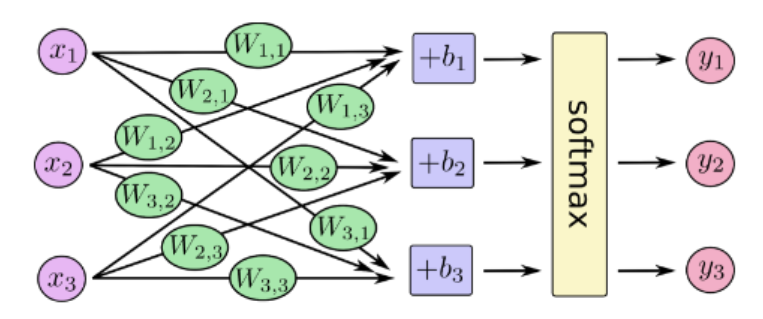
하나의 샘플에 대한 데이터 변환의 구체적인 계산은 다음과 같다.
입력으로 3개의 특성을 받고 3개의 유닛을 거쳐 값을 도출해야한다.
$y_1$을 예로 들자면 아래와 같은 과정을 거친다.
softmax를 거쳐 나오는 값을 $\hat{y}_1$이라 하면
$\hat{y}1 = x_1 \cdot W{1,1} + x_2 \cdot W_{1,2}+ x_3 \cdot W_{1,3}$이 된다.
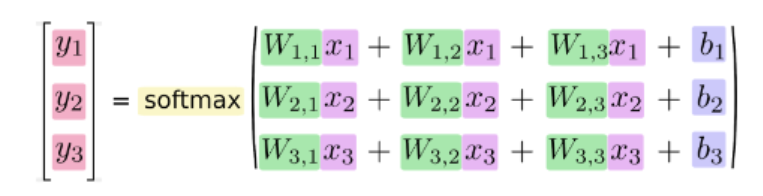
위 변환식을 행렬 연산으로 표현하면 다음과 같다.
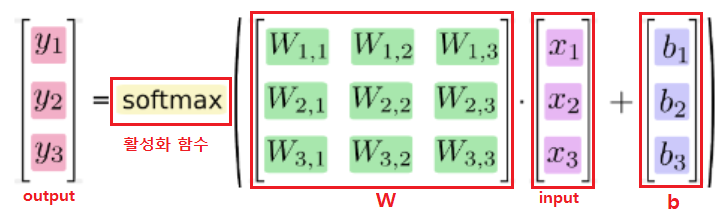
그림 출처: MNIST For Machine Learning Beginners With Softmax Regression
- 이런 식으로 행렬 계산을 사용해 배치 크기인 128개를 계산한다.
스텝과 훈련
- 배치 단위로 입력 데이터를 변환함
- 배치 크기 = 1step
-
예제: 마지막 층에서의 변환
1
softmax(W X + b)
- 1층에서는
softmax대신Relu라고 한다. - 훈련: 배치 단위로 예측 결과의 오차를 이용하여 가중치 행렬
W조정 -
학습 목표:
w, b -
아핀 변환과 데이터 변환
- 아핀 변환
- 회귀 모델에서는 활성함수(Softmax)가 없다. ⇒ 임의의 값을 도출해야 하기 때문
-
분류 모델은 정확한 값을 도출해야 하기 때문에 있다.
1
W X + b
- 신경망 모델에서 층과 층 사이의 데이터 변환: 아핀 변환 + 활성화 함수
- 위 예제에서는 아핀변환이 특성 → Relu → Softmax 총 2번 적용됐다.
2. 신경망 모델 훈련의 핵심 요소
-
요소
- 가중치
- 순전파 (예측값 만듦)
- 손실 함수 (loss)
- 역전파 (가중치 업뎃)
- 경사하강법 (옵티마이저)
- 옵티마이저
- 훈련 루프
-
가중치와 순전파
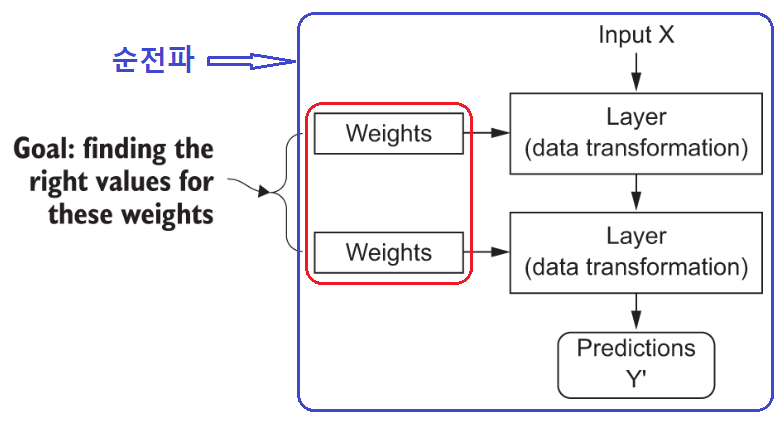
그림 출처: Deep Learning with Python(2판)
- 1층과 2층의 가중치는 서로 다르다
- input X는 1개의 배치임 즉, 128개란 소리
- 최초로 모델 실행시 가중치를 초기화하고 입력 데이터를 각 층에 전파해 예측값을 생성한다.
-
손실 함수
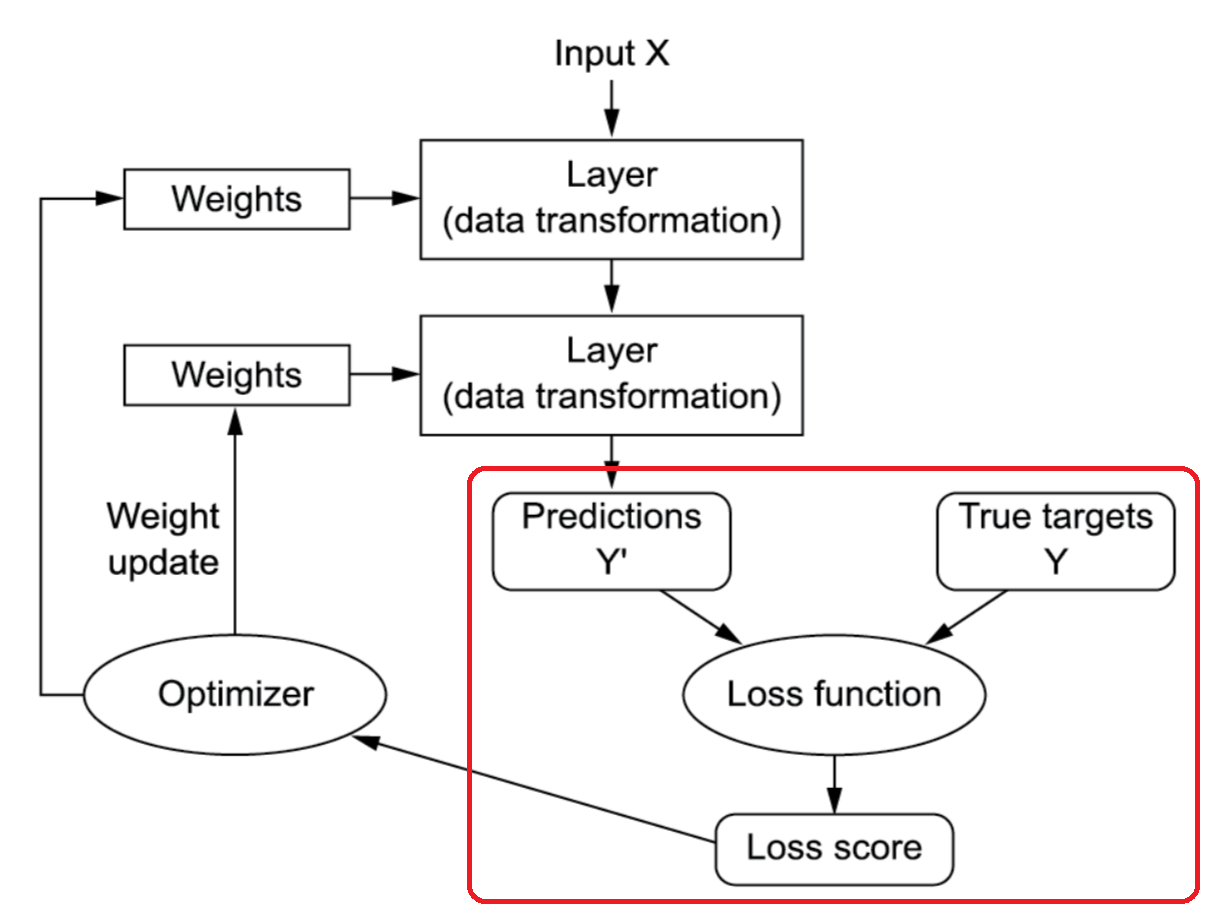
그림 출처: Deep Learning with Python(2판)
예측값과 실제 타겟 값을 가지고 손실 함수로 손실률을 계산한다.
-
역전파, 경사하강법, 옵티마이저
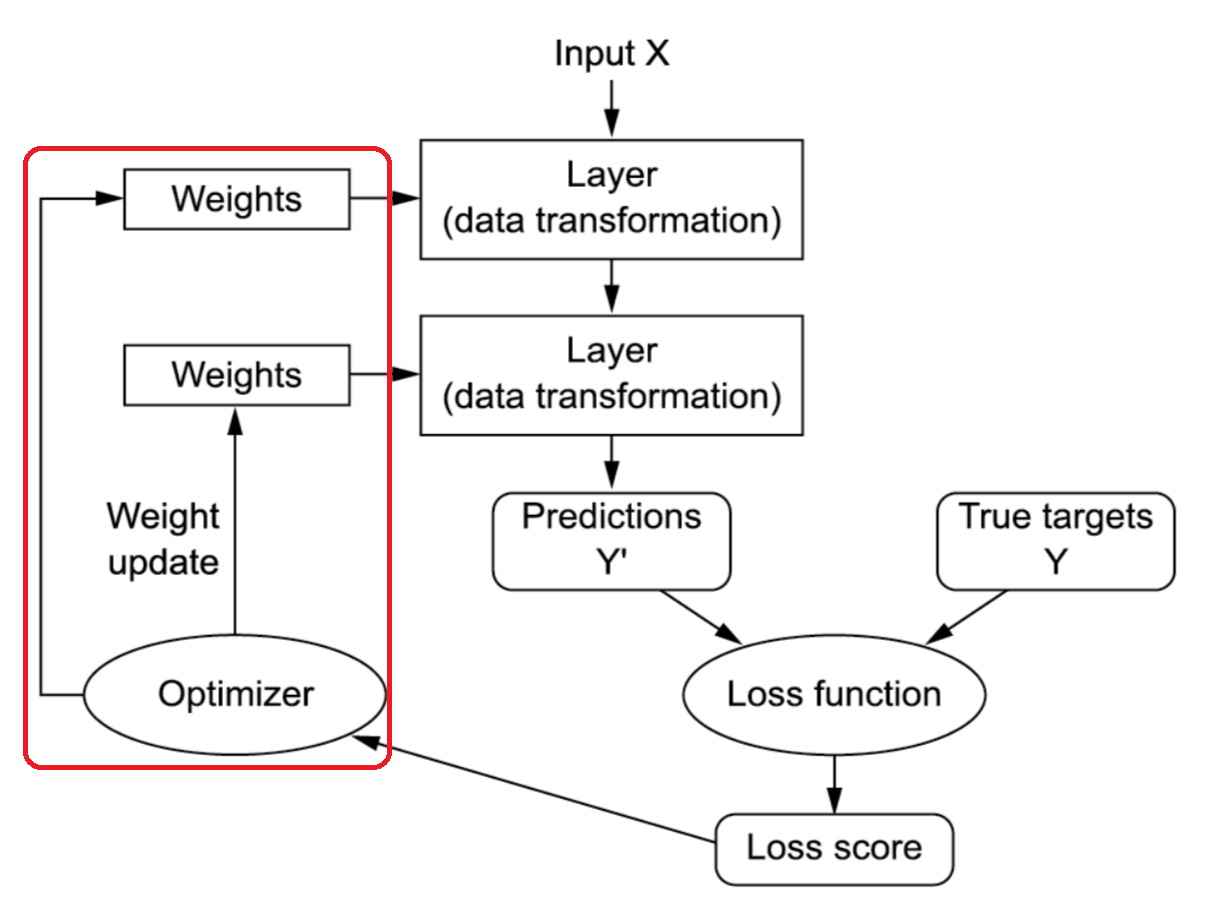
그림 출처: Deep Learning with Python(2판)
손실 함수 $w_1, w_2$의 미분 가능한 함수
기존에 $W_1, W_2$를 예측했으나 Loss 함수를 통해 새로운 $w_1, w_2$가 나온다면 옵티마이저를 사용해 $w_1, w_2$를 새로운 가중치로 업데이트함
훈련 루프
1
2
3
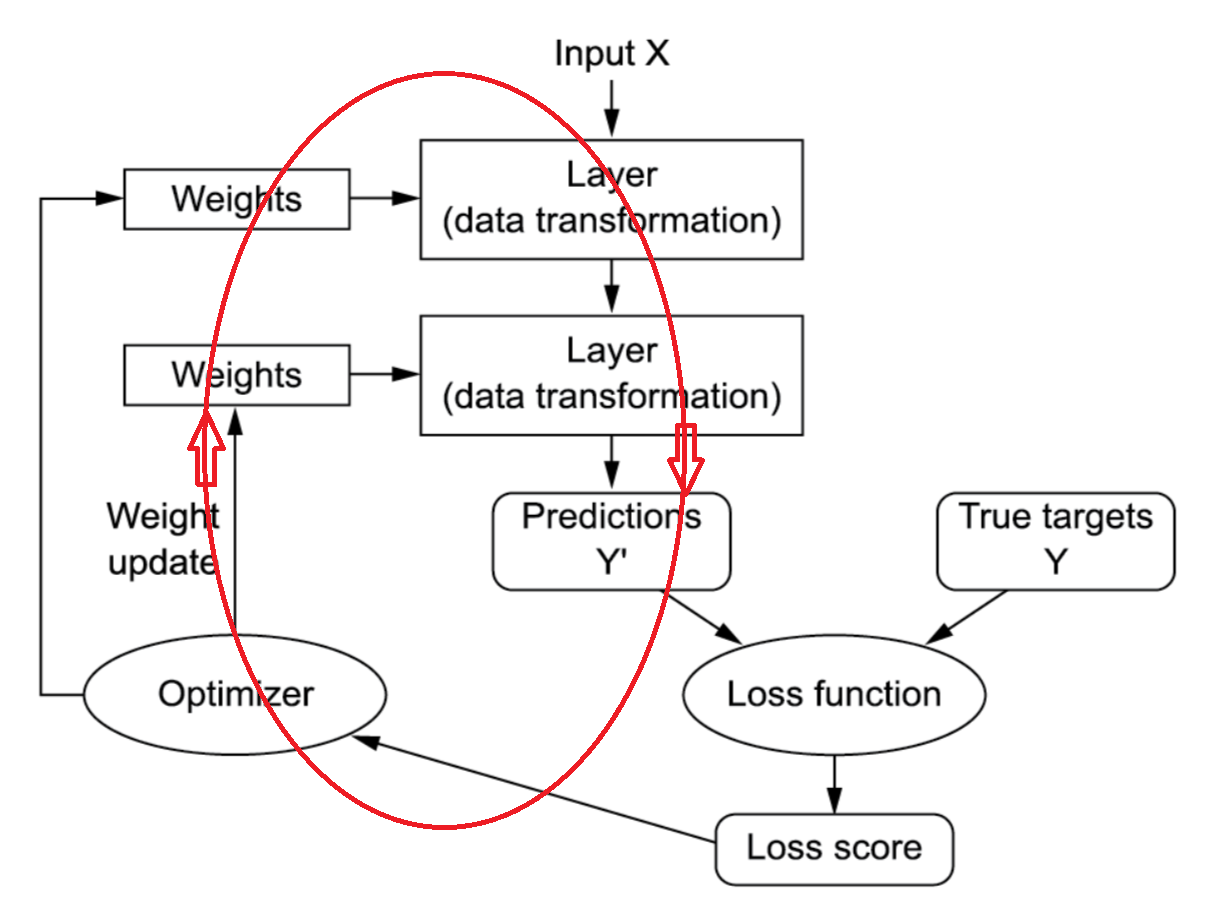
그림 출처: [Deep Learning with Python(2판)](https://www.manning.com/books/deep-learning-with-python-second-edition)
3. 훈련된 모델 활용과 평가
모델 활용
1
2
test_digits = test_images[0:10]
predictions = model.predict(test_digits)
1
predictions[0]

1
predictios[0].argmax()

1
predictions[0][7]

1
test_labels[0]

모델 성능 평가
1
2
3
4
```python
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(f"test_acc: {test_acc}")
```

4. 텐서 소개
텐서
- 넘파이 어레이
numpy.ndarray- 대표적인 텐서tensor 자료형
- 머신러닝에 사용되는 데이터셋은 일반적으로 텐서로 저장됨
- 텐서플로우
Tensor자료형인tensorflow.Tensor- 넘파이 어레이와 유사하며 GPU를 활용한 연산 지원
- 케라스 신경망 모델의 입력, 출력값
- 넘파이 어레이를 기본으로 사용
- 내부적으로는
tf.Tensor로 변환해서 사용
-
텐서의 차원
- 텐서의 표현에 사용된 축$_{axis}$의 개수
- 랭크$_{rank}$로도 불림
- 0차원(0D) 텐서 (랭크-0 텐서)
- 정수 한 개, 부동소수점 한 개 등 하나의 수를 표현하는 텐서.
-
스칼라$_{scalar}$라고도 불림.
1 2 3
np.array(12) np.array(1.34)
- 1차원(1D) 텐서 (랭크-1 텐서)
- 수로 이루어진 리스트 형식의 텐서.
- 벡터vector로 불리며 한 개의 축을 가짐.
1 2 3
np.array([12, 3, 6, 14, 7])
- 2차원(2D) 텐서 (랭크-2 텐서)
- 행과 열 두 개의 축을 가짐.
- 행렬$_{matrix}$로도 불림.
1 2 3
np.array([[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]])
-
2D 텐서 예제: 흑백 사진 데이터

그림 출처: Towards data science: Mikkel Duif(2019)
- 3차원(3D) 텐서 (랭크-3 텐서)
- 행, 열, 깊이 세 개의 축 사용.
- 동일 모양의 2D 텐서로 구성된 벡터로 이해 가능.
1 2 3 4 5 6 7 8 9 10 11
np.array([[[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]], [[5, 78, 2, 34, 0], [6, 79, 3, 35, 1], [7, 80, 4, 36, 2]]])
- 3차원(3D) 텐서 (랭크-3 텐서)
-
3D 텐서 예제: 컬러 사진 데이터


그림 출처: Machine Learning - Going Furthur with CNN Part 2
- 4D 텐서 (랭크-4 텐서)
- 3D 텐서로 이루어진 벡터
- 예제
- 컬러 사진 데이터로 구성된 훈련셋
- 동영상: 연속된 컬러 사진의 데이터셋으로 간주 가능
-
주의사항: 벡터의 차원
- 벡터의 길이를 차원이라 부르기도 함
- 예제:
np.array([12, 3, 6, 14, 7])는 5차원 벡터
- 4D 텐서 (랭크-4 텐서)
-
텐서 주요 속성
- 예제:
train_images가 MNIST의 훈련셋을 가리킴 -
ndim속성: 텐서의 차원 저장.1
train_images.ndim
-
shape속성: 텐서의 모양을 튜플로 저장.1 2 3 4 5
>>> train_images.shape (60000, 28, 28)
-
dtype속성: 텐서에 포함된 항목의 통일된 자료형.1 2 3 4 5
>>> train_images.dtype uint8
-
인덱싱
1 2 3 4
import matplotlib.pyplot as plt digit = train_images[4] plt.imshow(digit, cmap=plt.cm.binary) plt.show()
-
슬라이싱
-
첫째 배치
1
batch = train_images[:128]
-
둘째 배치
1
batch = train_images[128: 256]
-
n번째 배치1
batch = train_images[128 * n:128 * (n + 1)]
-
- 예제:
텐서 실전 예제
-
2D 텐서 예제
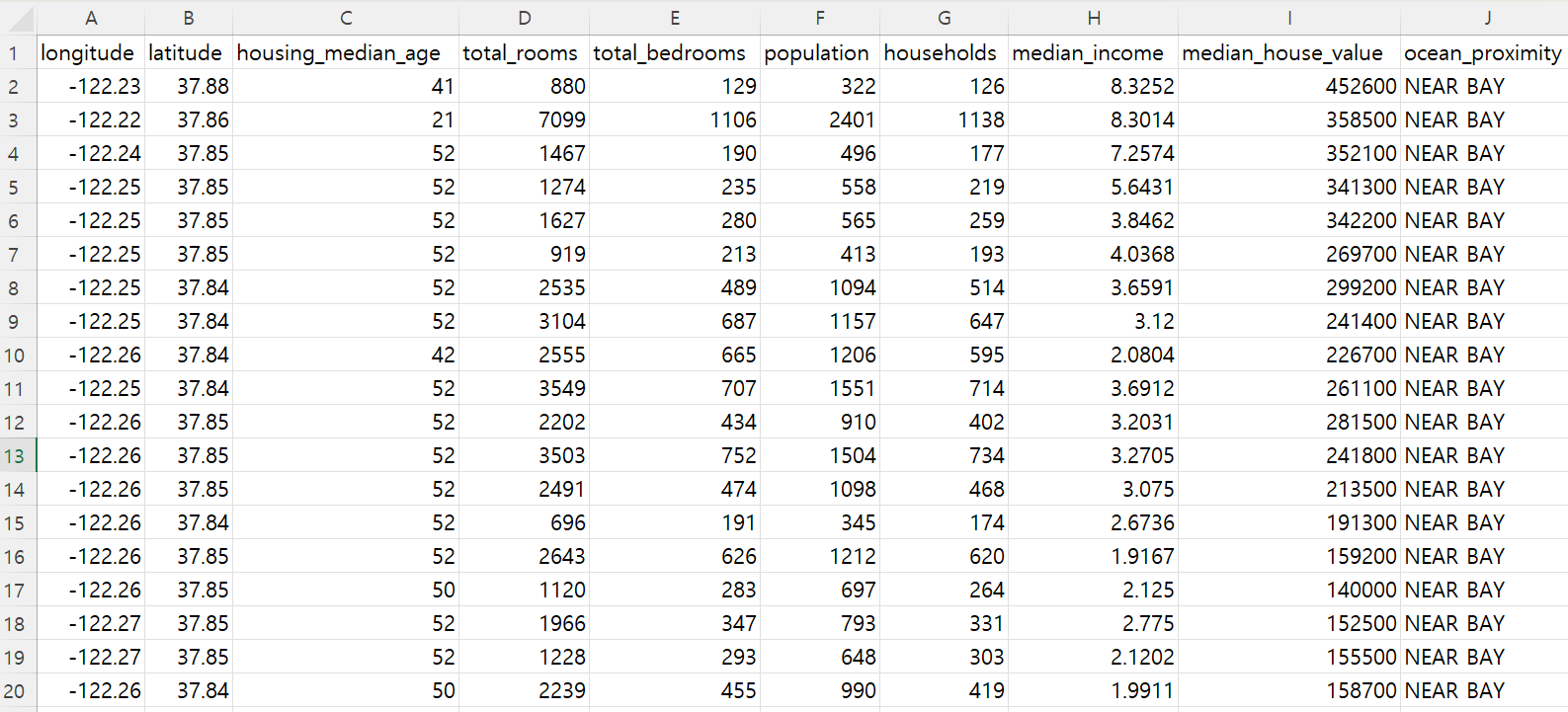
- 예제 1: 캘리포니아 구역별 인구조사 데이터셋
- 20,640개의 구역별 데이터 포함. 따라서
(20640, 10)모양의 2D 텐서로 표현 가능.
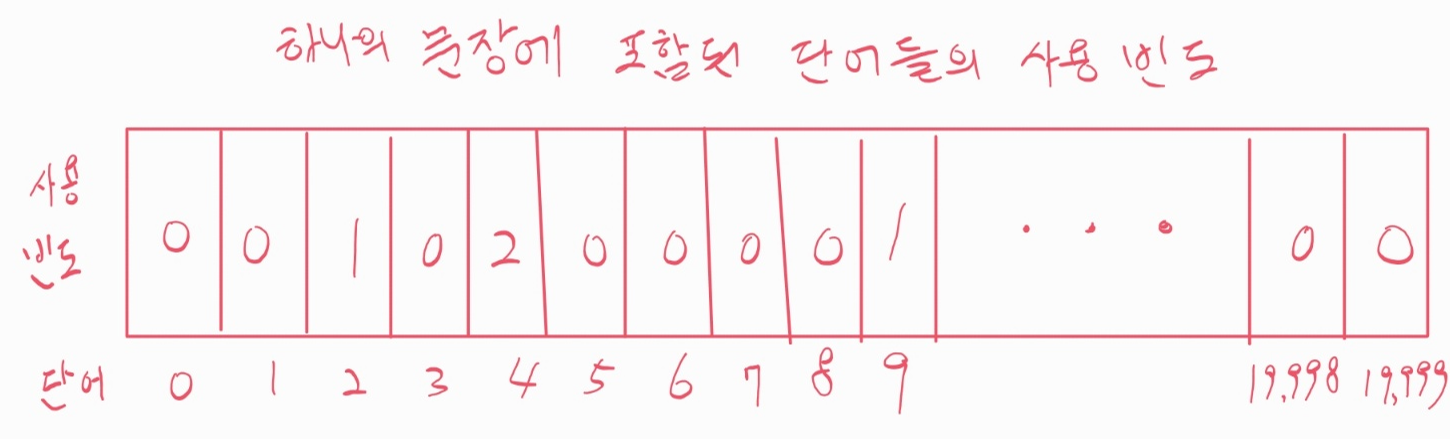
- 예제 2: 샘플: 문장에 사용된 단어들의 빈도를 모아놓은 벡터.
- 사용 가능 단어 2만 개
- 단어 각각이 지정된 문장에 사용된 빈도 측정
- 하나의 문장:
(20000,)모양의 벡터로 표현

- 데이터셋: 10만 개의 문장으로 구성된 데이터셋은
(100000, 20000)모양의 2D 텐서로 표현
-
3D 텐서 예제
- 시계열 데이터와 순차 데이터

그림 출처: Deep Learning with Python(2판)
-
예제 1: 1분마다 하루 총 390번 (현재 증시가, 지난 1분 동안 최고가, 지난 1분 동안 최저가)를
측정한 데이터 샘플
-
(390, 3)모양의 2D 텐서로 표현.

- 250일 동안 측정한 데이터셋은
(250, 390, 3)모양의 3D 텐서로 표현. - 예제 2: 하나의 트위터 데이터(트윗)는 최대 280개의 문자로 구성되고, 사용할 수 있는 문자가 총 128 개
- 트위터 샘플:
(280, 128)모양의 2D 텐서로 표현 가능함. - 각각의 항목은 128개의 문자 각각의 사용여부를 확인해주는 0 또는 1.
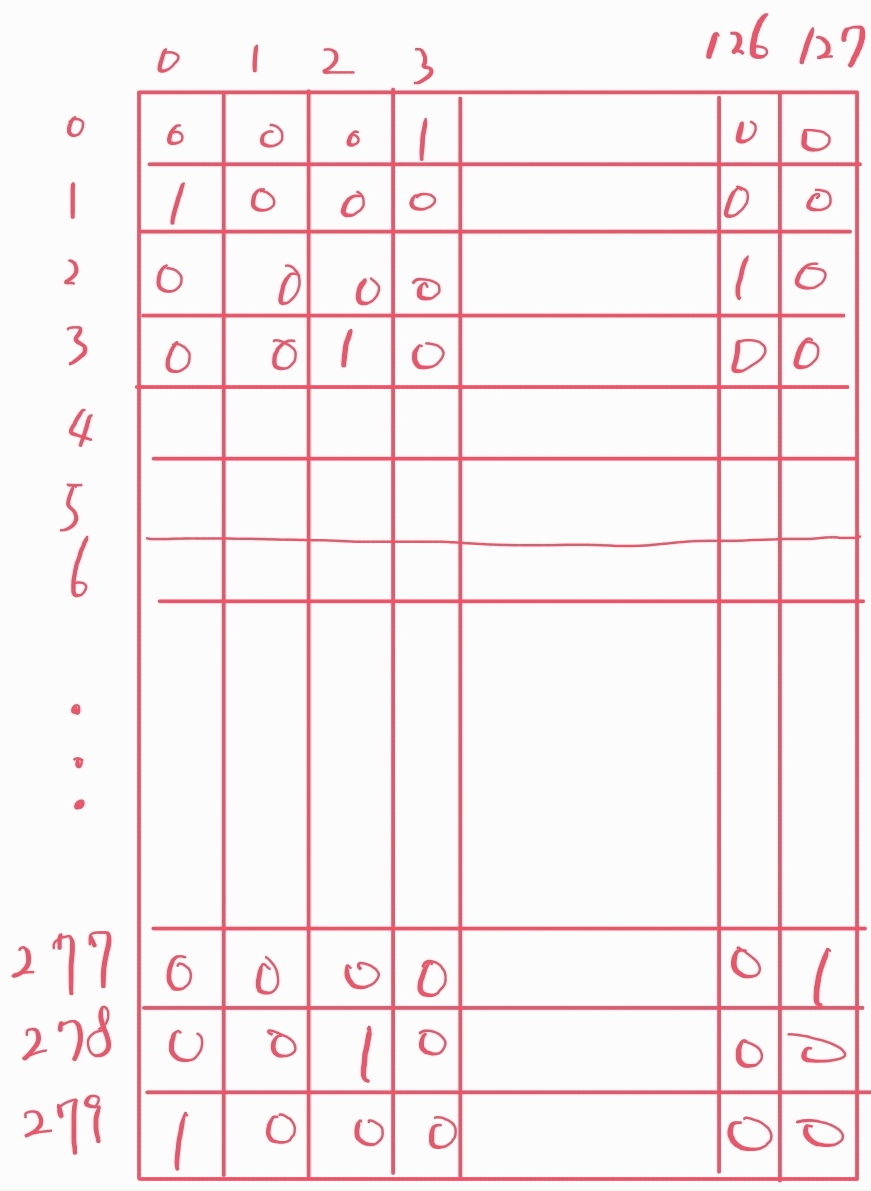
- 데이터셋: 백만 개의 샘플로 구성된 트위터 데이터셋은
(1000000, 280, 128)모양의 3D 텐서로 표현 가능.
-
4D 텐서 예제
-
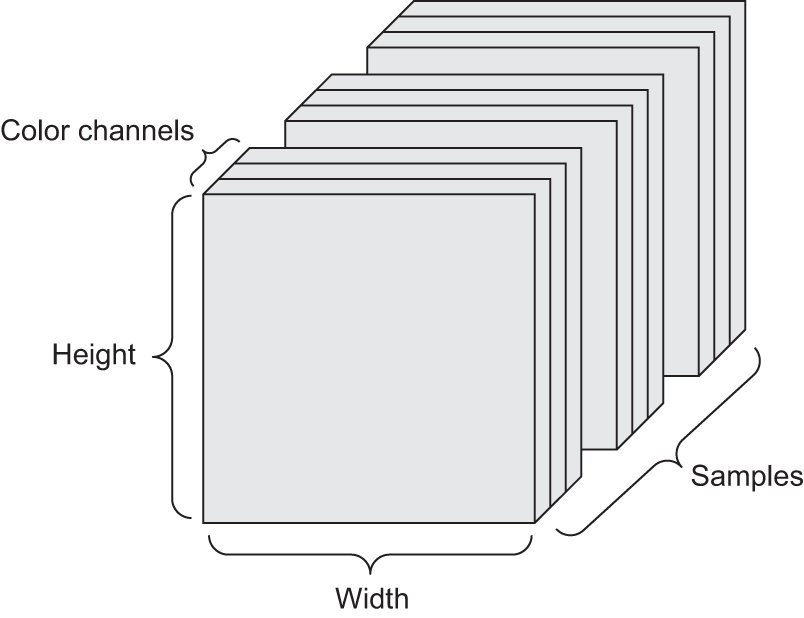
컬러 사진으로 구성된 데이터셋:
(샘플 수, 높이, 너비, 채널 수)또는(샘플 수, 채널 수, 높이, 너비)모양의 4D 텐서로 표현
-
텐서 연산
1
2
keras.layers.Dense(512, activation="relu")
keras.layers.Dense(10, activation="softmax")
- 첫째 층
W1: 첫째 층에서 학습되는 가중치 행렬b1: 첫째 층에서 학습되는 편향 벡터
output = relu(np.dot(input, W1) + b1) - 둘째 층
W2: 둘째 층에서 학습되는 가중치 행렬b2: 둘째 층에서 학습되는 편향 벡터
output = softmax(np.dot(input, W2) + b2) -
항목별 연산

그림 출처: Scipy Lecture Notes
-
유니버설 함수

그림 출처: Sharp Sight - How to Use the Numpy Maximum Function
텐서 연산의 기하학적 의미
- 이동: 벡터 합

- 회전: 점 곱

- 스케일링: 점 곱

- 아핀 변환

- 아핀 변환과 relu 활성화 함수

- 신경망의 텐서 연산

그림들 출처: Deep Learning with Python(2판)
5. 텐서플로우 텐서
- 종류
tensorflow.Tensortensorflow.Variable
tensorflow.Tensor자료형- 텐서플로우 라이브러리가 제공하는 텐서 자료형
np.ndarray와 매우 유사- 하지만 항목을 수정할 수 없는 불변 자료형
tf.Variable자료형- 모델 훈련에 사용되는 가변 자료형 텐서
- 가중치와 편향 텐서 등 값이 변하는 값들을 다루는 텐서
- 기타 성질은
tf.Tensor와 동일. - 다음 장에서 활용법 소개
- 스칼라: 랭크-0 텐서
1
2
3
4
5
6
import tensorflow as tf
import numpy as np
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
tf.Tensor(4, shape=(), dtype=int32)
1
rank_0_tensor.shape
Tensor Shape([])
- 벡터: 랭크-1 텐서
1
2
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
1
rank_1_tensor.shape
Tensor Shape([3])
- 행렬: 랭크-2 텐서
1
2
3
4
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)
tf.Tensor(
[[1. 2.]
[3. 4.]
[5. 6.]], shape=(3, 2), dtype=float16)
1
rank_2_tensor.shape
TensorShape([3, 2])
- 랭크-3 텐서
1
2
3
4
5
6
7
8
9
rank_3_tensor = tf.constant([
... [[0, 1, 2, 3, 4],
... [5, 6, 7, 8, 9]],
... [[10, 11, 12, 13, 14],
... [15, 16, 17, 18, 19]],
... [[20, 21, 22, 23, 24],
... [25, 26, 27, 28, 29]]
... ])
print(rank_3_tensor)
tf.Tensor(
[[[ 0 1 2 3 4]
[ 5 6 7 8 9]]
[[10 11 12 13 14]
[15 16 17 18 19]]
[[20 21 22 23 24]
[25 26 27 28 29]]], shape=(3, 2, 5), dtype=int32)
1
rank_3_tensor.shape
TensorShape([3, 2, 5])
- 랭크-3 텐서 이해 방식
rank_3_tensor의 모양: [3, 2, 5]

넘파이 어레이로의 변환
1
np.array(rank_2_tensor)
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
또는
1
rank_2_tensor.numpy()
array([[1., 2.],
[3., 4.],
[5., 6.]], dtype=float16)
텐서 연산
- 항목별 덧셈
1
2
3
4
5
6
a = tf.constant([[1, 2],
... [3, 4]])
b = tf.ones([2,2])
tf.add(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[2, 3], [4, 5]])>
또는
1
a + b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[2, 3], [4, 5]])>
- 항목별 곱셈
1
2
3
4
5
6
a = tf.constant([[1, 2],
... [3, 4]])
b = tf.ones([2,2])
tf.multiply(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[1, 2], [3, 4]])>
또는
1
a * b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[1, 2],b [3, 4]]>
- 행렬 연산
1
2
3
4
5
6
a = tf.constant([[1, 2],
... [3, 4]])
b = tf.ones([2,2])
tf.matmul(a, b)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[3, 3], [7, 7]])>
또는
1
a @ b
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[3, 3], [7, 7]])>
- 최대 항목 찾기
1
2
3
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
tf.reduce_max(c)
<tf.Tensor: shape=(), dtype=float32, numpy=10.0>
- 최대 항목의 인덱스 확인
1
2
3
4
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
tf.math.argmax(c)
<tf.Tensor: shape=(2,), dtype=int64, numpy=array([1, 0], dtype=int64)>
softmax()함수
1
2
3
c = tf.constant([[4.0, 5.0], [10.0, 1.0]])
tf.nn.softmax(c)
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=array([[2.6894143e-01, 7.3105860e-01], [9.9987662e-01, 1.2339458e-04]], dtype=float32)>
- 텐서 자동 변환
연산 결과는 기본적으로 tf.Tensor로 반환된다.
1
tf.convert_to_tensor([1,2,3])
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([1, 2, 3])>
1
tf.reduce_max([1, 2, 3])
<tf.Tensor: shape=(), dtype=int32, numpy=3>
1
tf.math.argmax([1, 2, 3])
<tf.Tensor: shape=(), dtype=int64, numpy=2>
1
tf.nn.softmax(np.array([1.0, 12.0, 33.0]))
<tf.Tensor: shape=(3,), dtype=float64, numpy=array([1.26641655e-14, 7.58256042e-10, 9.99999999e-01])>
텐서의 모양, 랭크, 축, 크기
넘파이 어레이의 경우와 동일하다.
- 모양: 텐서에 사용된 각각의 축에 사용된 항목의 개수로 구성된 벡터
- 랭크 또는 차원: 텐서에 사용된 축의 개수
- 스칼라의 랭크는 0,
- 벡터의 랭크는 1,
- 행렬의 랭크는 2.
- 축: 텐서 구성에 사용된 축
- 크기: 텐서에 포함된 항목의 개수
랭크-4 텐서 이해
1
rank_4_tensor = tf.zeros([3, 2, 4, 5])

1
rank_4_tensor.dtype
tf.float3
1
rank_4_tensor.ndim
4
1
rank_4_tensor.shape
TensorShape([3, 2, 4, 5])
1
rank_4_tensor.shape[0]
3
1
rank_4_tensor.shape[-1]
5
1
tf.size(rank_4_tensor)
<tf.Tensor: shape=(), dtype=int32, numpy=12
1
tf.rank(rank_4_tensor)
<tf.Tensor: shape=(), dtype=int32, numpy=4>
1
tf.shape(rank_4_tensor)
<tf.Tensor: shape=(4,), dtype=int32, numpy=array([3, 2, 4, 5])>
-
인덱싱/슬라이싱
넘파이 어레이의 경우와 동일하다.
1
rank_3_tensor[:, :, 4]
<tf.Tensor: shape=(3, 2), dtype=int32, numpy=array([[ 4, 9], [14, 19], [24, 29]])>
모양 변환
-
항목 저장 순서
1
rank_3_tensor
1
tf.reshape(rank_3_tensor, [-1])
<tf.Tensor: shape=(30,), dtype=int32, numpy=array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29])>-
축의 순서를 고려하는 좋은 모양 변환
전체 항목의 수를 유지하면서 축별 길이를 고려하는 모양 변환이 유용하다.
1
tf.reshape(rank_3_tensor, [3*2, 5])
<tf.Tensor: shape=(6, 5), dtype=int32, numpy= array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19], [20, 21, 22, 23, 24], [25, 26, 27, 28, 29]])>
- -1은 나머지 항목수를 자동으로 정하라는 의미이다.
1
tf.reshape(rank_3_tensor, [3, -1])
<tf.Tensor: shape=(3, 10), dtype=int32, numpy= array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9], [10, 11, 12, 13, 14, 15, 16, 17, 18, 19], [20, 21, 22, 23, 24, 25, 26, 27, 28, 29]])>
-
축의 순서를 고려하지 않는 나쁜 모양 변환
전체 항목의 수 또는 축 별 크기를 고려하지 않는 모양 변환은 의미가 없다.
1 2 3 4 5 6 7
tf.reshape(rank_3_tensor, [2, 3, 5]) tf.reshape(rank_3_tensor, [5, 6]) try: tf.reshape(rank_3_tensor, [7, -1]) except Exception as e: print(f"{type(e).__name__}: {e}")

-
텐서 항목의 자료형(
dtype) 변환생성된 텐서 항목의 자료형을 임의로 지정할 수 있다.
1 2
the_f64_tensor = tf.constant([2.2, 3.3, 4.4], dtype=tf.float64) the_f64_tensor
<tf.Tensor: shape=(3,), dtype=float64, numpy=array([2.2, 3.3, 4.4])>1 2
the_f16_tensor = tf.cast(the_f64_tensor, dtype=tf.float16) the_f16_tensor
<tf.Tensor: shape=(3,), dtype=float16, numpy=array([2.2, 3.3, 4.4], dtype=float16)>1 2
the_u8_tensor = tf.cast(the_f16_tensor, dtype=tf.uint8) the_u8_tensor
<tf.Tensor: shape=(3,), dtype=uint8, numpy=array([2, 3, 4], dtype=uint8)>
-
-
브로드캐스팅
넘파이 어레이의 경우와 동일하게 작동한다.
1 2 3 4 5
x = tf.constant([1, 2, 3]) y = tf.constant(2) z = tf.constant([2, 2, 2]) tf.multiply(x, 2)
tf.Tensor([2 4 6], shape=(3,), dtype=int32)1
x * y
tf.Tensor([2 4 6], shape=(3,), dtype=int32)1
x * z
tf.Tensor([2 4 6], shape=(3,), dtype=int32)1 2 3 4
x = tf.reshape(x,[3,1]) y = tf.range(1, 5) x * y
<tf.Tensor: shape=(3, 4), dtype=int32, numpy= array([[ 1, 2, 3, 4], [ 2, 4, 6, 8], [ 3, 6, 9, 12]])>
다양한 종류의 텐서
-
비정형 텐서
벡터의 길이가 일정하지 않은 축이 사용되는 텐서를 가리킨다.

1 2 3 4 5 6 7 8
ragged_list = [ [0, 1, 2, 3], [4, 5], [6, 7, 8], [9]] ragged_tensor = tf.ragged.constant(ragged_list) ragged_tensor
<tf.RaggedTensor [[0, 1, 2, 3], [4, 5], [6, 7, 8], [9]]>1
ragged_tensor.shape
(4, None) -
희소 텐서
텐서의 크기가 매우 큰 반면에 0이 아닌 항목의 개수가 상대적으로 적을 때 사용한다.

1 2 3 4 5
sparse_tensor = tf.sparse.SparseTensor(indices=[[0, 0], [1, 2]], values=[1, 2], dense_shape=[3, 4]) sparse_tensor
SparseTensor(indices=tf.Tensor([[0 0] [1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64)) -
밀집 텐서 대 희소 텐서
필요에 따라 자동으로 변환되지만 지정할 수도 있다.
1 2
dense_tensor = tf.sparse.to_dense(sparse_tensor) dense_tensor
<tf.Tensor: shape=(3, 4), dtype=int32, numpy= array([[1, 0, 0, 0], [0, 0, 2, 0], [0, 0, 0, 0]])>1
tf.sparse.from_dense(dense_tensor)
SparseTensor(indices=tf.Tensor( [[0 0] [1 2]], shape=(2, 2), dtype=int64), values=tf.Tensor([1 2], shape=(2,), dtype=int32), dense_shape=tf.Tensor([3 4], shape=(2,), dtype=int64))

댓글남기기